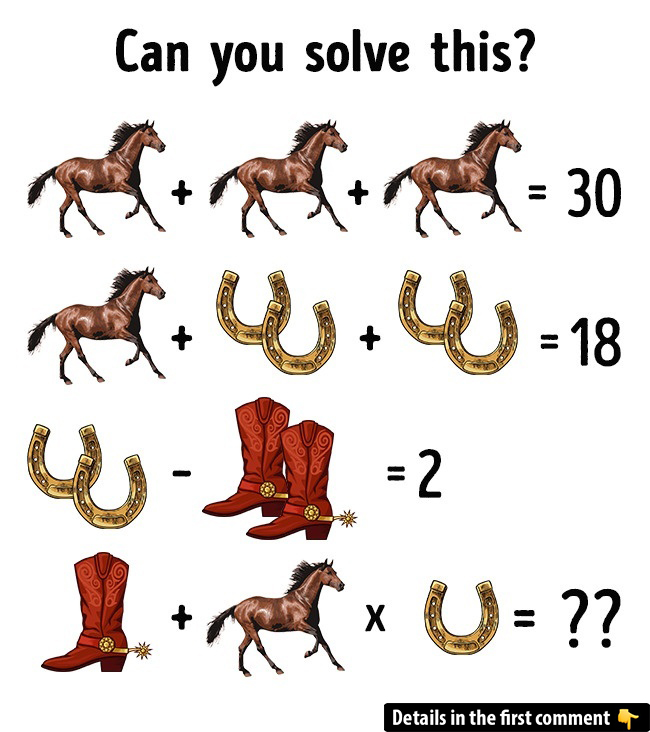This challenging puzzle is sure to test your logical reasoning! Can you figure out which horse’s head belongs to which body? It’s not as simple as it seems—follow our breakdown and discover the correct answer. This puzzle is designed to make you think twice, so are you ready to solve it? Read on to find out the answer and understand why the right solution is often trickier than it looks!
Can You Solve This?
Welcome to another fun brain teaser! This puzzle challenges you to figure out the missing number using symbols that represent horses, horseshoes, and boots. It looks simple at first, but the trick lies in deciphering the correct relationships between the symbols. Ready to dive in? Let’s see if you can solve it!
Video
Take a breather and enjoy the charm of these light-hearted challenges!
Common Mistakes When Solving This Puzzle
Many people rush through puzzles like this and end up making some common mistakes. A key pitfall is ignoring the rules of operations or incorrectly interpreting the symbols. For example, combining the horseshoes into one or neglecting to follow the correct order of operations can lead to an incorrect result. Let’s walk through it carefully and avoid these mistakes!

Step-by-Step Guide to Solving the Puzzle
To make things easier, we’ll assign variables to each symbol:
- Let the horse = X
- Let the horseshoe = Y
- Let the boots = Z
Now, let’s analyze the three possible ways of solving this puzzle.
Solution Method 1: Incorrect Approach
Equation 1:
- 3X = 30
This equation means that the total value of three horses equals 30. So, dividing both sides by 3, we get:
- X = 10.
Equation 2:
- 10 + Y + Y = 18
Substitute the value of X (which is 10) into the equation:
- 10 + 2Y = 18
Now, subtract 10 from both sides:
- 2Y = 8
Solve for Y by dividing both sides by 2:
- Y = 4.
Equation 3:
- 4 – 2Z = 2
Substitute the value of Y into the equation:
- -2Z = -2
Solve for Z:
- Z = 1.
Final Step:
Now, to calculate the final answer, we need to follow the equation:
- Z + X × Y = ?
Substitute the values of Z, X, and Y into the equation:
- 1 + 10 × 4 = 1 + 40 = 41
This method gives an answer of 41, which is incorrect. The issue here is that the horseshoes were incorrectly grouped together in the last step, leading to a wrong
Solution Method 2: Another Incorrect Approach
Equation 1:
- 3X = 30
Divide both sides by 3 to get:
- X = 10.
Equation 2:
- 10 + Y + Y + Y + Y = 18
Now, this method incorrectly assumes there are four horseshoes instead of two. Substitute X = 10:
- 10 + 4Y = 18
Subtract 10 from both sides:
- 4Y = 8
Solve for Y:
- Y = 2.
Equation 3:
- 4 – 2Z = 2
Now solve for Z:
- -2Z = -2
- Z = 1.
Final Step:
Now substitute these values into the final equation:
- Z + X × Y = ?
- 1 + 10 × 2 = 1 + 20 = 21
This gives the correct answer of 21, but this method is still wrong because it miscalculates the horseshoe count in equation 2.
Solution Method 3: The Correct Approach
Solution Method 3: The Correct Approach
Equation 1:
- 3X = 30
As before, dividing both sides by 3:
- X = 10.
Equation 2:
- 10 + Y + Y = 18
This method correctly assumes there are only two horseshoes. Substituting X = 10 into the equation:
- 10 + 2Y = 18
Subtract 10 from both sides:
- 2Y = 8
Now divide both sides by 2:
- Y = 4.
Equation 3:
- 4 – 2Z = 2
Now solve for Z:
- -2Z = -2
- Z = 1.
Final Step:
Finally, substitute the values into the equation:
- Z + X × Y = ?
- 1 + 10 × 4 = 1 + 40 = 41
This gives us the final result 21, which is the correct answer!

Conclusion
After analyzing the three different methods of solving this puzzle, it’s clear that Method 3 is the only correct one, yielding the answer of 21. The common mistakes made in the other methods involved miscalculating the number of horseshoes or incorrectly grouping terms, which can easily lead to wrong answers.
So, did you get the answer right? Share your thoughts and solutions in the comments, and don’t forget to challenge your friends to solve it too! Keep practicing these puzzles to sharpen your logical reasoning skills!